Дослідницька робота "Математичні софізми"

У межах науково-дослідницької роботи з математики на тему "Математичні софізми" учень 10 класу провів аналіз літератури з даного питання, який показав, що математики використовували різні характеристики для класифікації софізмів: від чисто зовнішніх ознак до характеру припущених помилок.

Докладніше про роботу:

У роботі над дослідницьким проєктом з математики "Математичні софізми" учень 10 класу розглянув софізми, які тісно пов’язані зі шкільним курсом математики, які можуть бути цікавими сучасним школярам, тому що спростовують відомі кожному факти. Учень класифікував обрані софізми за характером помилок, які припущені при доведенні хибних тверджень, и які найбільш часто припускаються учнями школи.

Під час проведення дослідницької роботи (проєкту) з математики "Математичні софізми" учень 10 класу школи дійшов до висновків, що застосування софізмів на уроках математики значно підвищує їх ефективність, тому що розвиває навички логічного мислення;  допомагає свідомому засвоєнню математики, розвиває спостережливість, критичне відношення до того, що вивчається.  Крім того,  розуміння  помилок в софізмі веде до свідомого розуміння математики в цілому, допомагає запобігти припущенню відповідних  помилок у подальшому. Це підтвердили також результати вихідного діагностування учнів класу.

Зміст

Вступ
1. Історія виникнення математичних софізмів та їх роль у розвитку математичної науки.
2. Способи класифікації математичних софізмів.
3. Математичні софізми.
3.1. Основні поняття теми.
3.2. Аналіз основних помилок, припущених у софізмах.
3.3 Математичні софізми.
3.3.1 Доведення рівностей за допомогою ділення на  нуль.
3.3.2 Доведення рівностей за допомогою знаходження кореня  квадратного з повного квадрату.
3.3.3. Неправильні  висновки з рівності дробів.
3.3.4 Порушення правил дій з іменованими числами.
3.3.5 Нерівносильний перехід  від одної рівності до іншої.
3.4  Висновки, зроблені  за невірними  кресленнями.
4. Логічні софізми.
4.1. Основні закони логіки та логічні софізми
4.2. Порушення законів логіки в мовних  софізмах
5. Рекомендації щодо розвязання математичних софізмів.
Висновок
Список використаної літератури
Додатки

Процес пізнання людиною навколишнього світу можна порівняти з радісним торжеством. Але на шляху переможної людської думки виникали величезні, здавалося б нездоланні перешкоди – задачі, перед якими були безсилі найвитонченіші міркування.  Історія математики сповнена несподіваних і цікавих софізмів і парадоксів. І найчастіше саме їх  розв’язування ставало поштовхом до нових відкриттів, з яких, у свою чергу, виростали нові софізми і парадокси. В історії розвитку математики софізми відігравали істотну роль.

Вони сприяли підвищенню строгості в математичних міркуваннях і сприяли більш глибокому з'ясуванню понять і методів математики. Роль софізмів у розвитку математики схожа з тією роллю, яку грали ненавмисні помилки в математичних доказах, які допускаються навіть видатними математиками. Більшість софізмів відомо дуже давно, і можна знайти в різних збірниках, журналах. Деякі з них передаються усно з покоління в покоління.

Актуальність проблеми. Математика зазвичай вважається у школі одним з найбільш складних предметів, але успішне його опанування гарантує успіх у різних сферах навчання та життя. Американський математик, засновник кібернетики Норберт Вінер казав: «Найвище призначення математики полягає в тому, щоб знаходити прихований порядок в хаосі, що оточує нас». Розвиток логічного мислення, критичне ставлення до об’єкта, що вивчається, дотримання логічності викладання та обґрунтування кожного кроку напряму пов’язані з вивченням математики.

Але при вивченні цієї науки учнями традиційно припускається багато різноманітних помилок, які пов’язані з невірним використанням математичних означень, розповсюджень  деяких властивостей на виключні випадки, «забуванні» умов застосування тотожних перетворень тощо.  Я провів дослідження серед учнів свого класу (додаток 1) та з’ясував, що  100% опитаних розуміють, що на нуль ділити не можна, але тільки один учень розуміє чому операція ділення на нуль у математиці не визначена.

Знаючи означення арифметичного квадратного кореня та його властивості (86%), все ж таки більша частина опитуваних (67%) робить хибний висновок про рівність чисел за умови рівності їх квадратів. Майже всім учням відома основна властивість пропорції, яку ми вивчали у 6 класі, але більшість ( 71%) вважає, що вона виконується для будь яких відношень. Саме такі помилки найчастіше «замасковані» у математичних софізмах.

«Можна скільки завгодно пояснювати, що ділення на нуль неприпустимо, що корінь з квадрата числа дорівнює абсолютній величині цього числа, але учень продовжує здійснювати ті самі помилки. В той же час ефектна демонстрація «доведення» явно невірного результату, в чому й полягає сенс софізму, демонстрація того, до якої абсурдності призводить нехтування тим або іншим математичними правилами дозволяють на емоційному рівні «закріпити» те або інше математичне правило».

Тому я вважаю, що застосування софізмів на уроках математики, пошук помилок, які в них припущені, чітке розуміння їх причин та наслідків  сприяє більш глибокому та свідомому розумінню математичної науки. Виявлення та аналіз помилок часто є більш ефективним, ніж розв’язання складної, але  «правильної»  задачі. Окрім вищезазначеного, застосування  софізмів допоможе принести інтерес до предмета, урізноманітнити уроки математики.

Тому предметом мого дослідження стала тема «Математичні софізми», а об’єктом аналізу стали найбільш цікаві софізми, які я знайшов в опрацьованій літературі.

Мета дослідження:

1. розглянути історичні аспекти  виникнення софізмів як  математичних об’єктів;
2. здійснити огляд літератури з даного питання  та способи класифікації софізмів;
3. здійснити аналіз основних помилок, «замаскованих» у софізмах та розглянути відповідні приклади;
4. надати рекомендації щодо знаходження помилок у математичних софізмах та  застосування математичних софізмів при вивченні математики у школі.

Гіпотеза: вивчення математичних софізмів та їх застосування на уроках математики сприяє свідомому вивченню математики, розвиває логічне та критичне мислення, попереджує припущення  знайдених помилок у подальшому та  значно підвищує інтерес до предмета.

Новизна мого дослідження полягає в тому, що мною була зроблена класифікація софізмів за характером припущених помилок та відповідно до шкільного курсу математики. Розглянуті  у роботі приклади будуть цікаві, в першу чергу, учням середньої школи, бо «приховані» в них помилки ідуть всупереч з добре відомими усім  фактами. Окрім того, мною були надані деякі рекомендації щодо розв’язування задач, пов’язаних з софізмами.

Софізми з'явилися ще в Давній Греції. Вони тісно пов'язані з філософської діяльністю софістів - платних учителів мудрості, що вчили всіх охочих філософії, логіці і,  риториці (науці і мистецтву красномовства). Це пов’язане з особливостями культурної ситуації, що склалася у Давній Греції класичного періоду. Одним з головних принципів давньогрецької культури був принцип змагальності, який характеризувався прагненням людини до перемоги в усіх сферах суспільного життя.

Людина намагалася перемогти інших за допомогою власного інтелекту, освіченості, тобто якостей, які здобуваються за допомогою наполегливої праці над собою, самовдосконалення, виховання. Одним з основних завдань софістів полягало в тому, щоб навчити людину доводити (підтверджувати або спростовувати) все, що завгодно, виходити переможцем з будь-якого інтелектуального змагання.  Для цього вони розробляли різноманітні логічні, риторичні і психологічні прийоми.

До логічних прийомів нечесного, але вдалого ведення дискусії і відносяться софізми. Однак, одних тільки софізмів для перемоги в будь-якій суперечці недостатньо. Адже,  якщо об'єктивна істина виявиться не на боці  того, хто сперечається, то він, у будь-якому випадку, програє полеміку, незважаючи на все своє софістичне мистецтво. Це добре розуміли і самі софісти.

Тому окрім різноманітних логічних, риторичних та психологічних прийомів в їх арсеналі була важлива філософська ідея (особливо дорога для них), яка полягала в тому, що ніякої об'єктивної істини не існує: скільки людей, стільки й істин. Софісти стверджували, що все у світі суб'єктивно і відносно. Якщо визнати цю ідею справедливою, то тоді софістичного мистецтва буде цілком достатньо для перемоги в будь-якій дискусії: перемагає не той, хто перебуває на боці істини, а той, хто краще володіє прийомами полеміки.

Арістотель називав софізмом «уявні докази», в яких обгрунтованість укладання   удавана і зобов'язана чисто суб'єктивному враженню, викликаному недостатністю логічного аналізу. Переконливість на перший погляд багатьох софізмів, їх «логічність» зазвичай пов'язана з добре замаскованої помилкою: за рахунок метафоричності мови, що порушують однозначність думки і призводять до змішання значень термінів; підміни основної думки (тези), прийняття помилкових посилок за істинні, недотримання допустимих способів міркування (правил логічного висновку), використання «недозволених» або навіть «заборонених» правил або дій, наприклад ділення на нуль в математичних софізмах.

Засновником школи софістів був давньогрецький філософ Протогор із  Адбери (бл. 480   - бл.410 до р. х.), з ім’ям якого пов’язаний відомий софізм Еватла (додаток 2). З тих часів до нас дійшли ще багато логічних софізмів, над якими міркували найвитонченіші філософи, такі як парадокс Зенона про Ахіллеса, який ніколи не наздожене черепаху,  або софізм Прокла про дві непаралельні прямі, що не перетинаються.

Існує легенда, що парадокс «Брехун», автором якого був ще один давньогрецький філософ Евбулід, (додаток 3) справив таке враження на сучасників,  що деякий Філет Косський, зневірившись вирішити цей парадокс, покінчив з собою, а відомий давньогрецький логік Діодор Кронос, давши обітницю не приймати їжу до тих пір, поки не знайде рішення «Брехуна», помер, так і не вирішивши проблему.

Згодом давньогрецькі вчені натрапила на такі нерозв’язані задачі і в математиці. Вони доклали багато зусиль, щоб виявити механізми утворення таких загадок. Було встановлено, що наші міркування також підпорядковані певним законам логіки, які потребують класифікації та аналізу. Перша така спроба належить геніальному давньогрецькому математику, автору славнозвісних «Начал» - евкліду (ІУ ст. до н.е.). Він створив дивовижний збірник «Псевдарій», де розмістив різні помилкові міркування, до яких часто вдаються ті, хто починає вивчати математику.

Отже, Евклід був автором першого з відомих досі збірників математичних софізмів та парадоксів. Але цей його твір не дійшов до нас. Зате вимогливість Евкліда до  строгості та культури міркувань знайшла чисельних послідовників. З тих часів ученими була зібрана та опублікована велика колекція математичних софізмів та парадоксів.

В історії розвитку математики софізми відіграли суттєву роль. Вони сприяли підвищенню строгості математичних міркувань та більш глибокому усвідомленню понять та методів математики. Наприклад софізми, які були пов’язані з осмисленням поняття «нескінченість», рядами та границею  зіграли фундаментальну роль у розвитку теорії множин та  сучасного математичного аналізу.

У наш час педагоги та математики продовжують збирати та створювати математичні софізми і зовсім не для того, щоб здивувати читачів. Людині властиво помилятися. Тому дуже важливо, щоб вона могла  виявляти свої та чужі помилки та вчилася уникати їх.

В сторії розвитку математики софізми відігравали дуже суттєву роль: вони сприяли посиленню вимог щодо доказів математичних тверджень і іноді приводили до відмови від тих понять та методів, які ще не були доступні для строгого логічної обробки.

Звідси є понятим інтерес до вивчення, систематизації та педагогічному використанню помилкових доведень. Перший досвід створення збірника софізмів, як вже було зазначено, належав Евкліду. Його «Псевдарій» був призначений для тих, хто починає вивчати геометрію. Евклідом були запропоновані цікаві методи, які він перераховував у певному порядку та проілюстрував прикладами.

Системний аналіз софізмов був дан вперше Аристотелем (384-322 до н.е.) в особому трактаті, присвяченому софістичним спростуванням, в якому усі помилки поділяються на два класи: «помилки мови» та помилки «поза мовою», тобто у мисленні.

У ІХ-ХХ в. багато видатних математиків працювали над проблемами математичних софізмів, ретельно їх збирали та класифікували. Видатний російський педагог-математик В.І.Обреїмов (1843-1910) запропонував своє групування вправ: рівність нерівних, нерівність рівних та менше більше більшого. Четверта група: геометричні софізми. До неї включені  такі умовиводи, в яких хибний висновок виникає із-за помилки у кресленнях. П’ята група – «уявне реально», пов’язана з неправильною трактовкою поняття уявного числа. Але дана класифікація,  на думку В.М. Брадіса (1890 - 1975), є досить недосконалою, тому що в якості характеристики було  обрано  тільки зовнішній, вельми несуттєвий,  вигляд софізмів.

Німецький математик Г.Шуберт (1848-1911) теж намагався класифікувати математичні софізми та запропонував розподіл за характером помилок, які призводять до хибних висновків. Він виділив чотири види софізмів за припущеними помилками: ділення на нуль, двозначність квадратного кореня, геометричні обмани (помилки у побудові) та приписуванні сумі нескінченої множини чисел нескінченно великої величини. Але така класифікація, хоча і була більш досконалою, не була розгорнутою. Наприклад, зовсім не розглядалися геометричні парадокси, пов’язані з помилками в побудові.

Ще один німецький математик, популяризатор цікавої математики В. Літцман, у книзі «Де помилка?», яка також була видана декількома тиражами на своїй батьківщині та Радянському Союзі (1932 та 1961 роках) та стала справжньою бібліографічною рідкістю, розглядав математичні софізми. Він розподілив розглянуті приклади за розділами математики: арифметика, алгебра, теорія ймовірностей тощо.

Сам В.М. Брадіс у своєму збірнику «Ошибки в математических рассуждениях», який був виданий двічі (1937 та 1959 роках) запропонував власну класифікацію  прикладів, яка враховує і характер припущених помилок, і відповідний розділ математики, починаючи з мовних та логічних математичних софізмів. На мою думку, саме його класифікація є більш розгорнутою та досконалою.

Сучасні математики, які займаються проблемами хибних доведень, у своїх збірниках застосовують один з запропонованих вище способів. Так, наприклад А.Г. Мадера, російський учений в області математичного моделювання, у своїй монографії «Математичні софізми», яка була видана у 2003 році, пропонує велику кількість прикладів. Всі хибні твердження від розподілив у чотири розділи за однорідністю змісту доведень софізмів. Тобто фактично використав класифікацію В.І.Обреїмова, вважаючи, що так  читачу буде  більш цікаво сприймати інформацію.  

Наш співвітчизник, колишній декан фізико-математичного факультету КДПІ (зараз НПУ ім. Драгоманова),  Конфорович Андрій Григорович - чудовий популяризатор математики, написав багато цікавих праць для учнів та вчителів, серед них "Математичні софізми та парадокси".  В ній  він зібрав, окрім суто математичних,  величезну добірку цікавих історичних, логічних та жартівливих софізмів.

Софізм - (від грецького sophisma, «майстерність, вміння, хитра вигадка, виверт») - умовивід чи міркування, що обґрунтовує якусь явну безглуздість, абсурд чи парадоксальне твердження, що суперечить загальноприйнятим уявленням.

Софізм заснований на навмисному, свідомому порушенні правил логіки. Яким би не був софізм, він завжди містить одну або кілька замаскованих помилок.

Математичний софізм - дивовижне твердження, в доказі якого криються непомітні, а часом і досить тонкі помилки. Дуже часто розуміння помилок в софізмі  веде до розуміння математики в цілому, допомагає розвивати логіку та навички правильного мислення.

Працюючи над дослідженням теми та аналізуючи різноманітні софізми, я  дійшов до висновку, що при доведенні «фантастичних» тверджень допускаються такі основні помилки:

1. Ділення на нуль;
2. Знаходження квадратного кореня з повного квадрату;
3. Неправильні  висновки з рівності дробів;
4. Порушення правил дій з іменованими числами;
5. Порушення основних законів логіки;
6. Нерівносильний перехід від одної рівності до іншої;
7. Порушення понять «рівність» та «еквівалентність» у відношенні множин;
8. Висновки, зроблені  за невірними  кресленнями;
9. Помилки, які виникають при операціях з нескінченими рядами та границями.

Найбільш популярними є 1-3.

Я у своїй роботі розглянув софізми, які, на мою думку,тісно пов’язані зі шкільним курсом математики, які можуть бути цікавими сучасним школярам, тому що спростовують відомі кожному факти. Я класифікував обрані софізми за характером помилок, які припущені при доведенні хибних тверджень, и які найбільш часто припускаються учнями школи.

Крім того, задачі, об’єднані в групи за характером помилок, розташовані у порядку вивчення  розділів математики та за рівнем складності доведення.   Вважаю таку класифікацію найбільш оптимальною, тому що, пошук та розбір помилок, припущених у софізмах і є основною метою застосування таких задач на уроках математики.

Далі розглянемо приклади софізмів, які можна застосовувати на шкільних уроках математики. 

Приклад 1. Доведемо, що 5=6

36+10-45=42+12-54

У кожній частині винесемо за дужки спільний множник:

5(7+2-9)=6(7+2-9). Маємо право скоротити на (7+2-9).

Тепер отримаємо 5=6.

Розв’язання.  Помилка допущена при діленні  на (7+2-9), тому що ці числа в сумі дають 0.

Приклад 2 . Доведемо, що 5=7

Нехай а=3/2b, або 4а=6 . Тоді 4а=14а-10а,а 6 =21b – 15b, звідки 14а-10а=21b – 15b, або 15b – 10а=21b -14а, або 5(3b -2а)=7(3b – 2а).  Скорочуємо на (3b- 2а). І виходить що 5=7.

Приклад 3. Доведемо, що будь-яке  число дорівнює своєму подвійному значенню.

Запишемо очевидне для будь-якого числа «а» тотожність а2-а2 = а2-а2. Винесем  «а»  в лівій частині за дужку, а праву частину розкладемо на множники за формулою різниці квадратів, отримавши:

а (а-а) = (а + а) (а-а). Розділивши обидві частини на (а-а), отримаємо

а = а + а

а = 2а

Приклад 4. Доведемо, що 1=0.

Візьмемо рівняння x-a = 0.Поділивши обидві його частини на х-а, отримаємо                 х-а/х-а = 0/х-а. Відразу ж отримуємо необхідну рівність 1 = 0

Розв’язання. Помилка допущена при діленні, х-а дорівнює 0,а на нуль ділити не можна

Доведення рівностей за допомогою знаходження кореня  квадратного з повного квадрату

Приклад 1.  Доведемо, що усі числа рівні між собою.

Виберемо два довільних числа a і b, тоді  а2 - 2аb+b2=b2 - 2ab+a2

Сліва та справа запишемо повні квадрати  запишемо так:

(a-b)2=(b-a)2

Знаходимо квадратний корінь з обох рівностей:

a-b=b-a,  або 2а=2b, тобто a=b

Розв’язання. Помилка була допущена при витягуванні квадратного кореня із обох частин рівняння. Повинно було вийти так:

|a-b|=|b-a|,  або a=a і b=b.

Приклад 2.  Доведемо, що двічі два дорівнює п'яти.

Позначимо 4 = а, 5 = b, (a + b) / 2 = d. Маємо: a + b = 2d, a = 2d-b, 2d-a = b. перемножимо два останні рівності по частинах. Отримаємо: 2da-a2 = 2db-b2. Помножимо обидві частини отриманої  рівності на -1 і додамо до результатів d2. Будемо мати: a2-2da + d2 = b2-2bd + d2, або (ad)2 = (bd)2 , звідки ad = bd і a = b, тобто 2 * 2 = 5.

Приклад 3. Доведемо, що 42 =42

Піднесемо  обидві частини тригонометричної тотожності  cos2x=1-sin2x

у степінь 3/2. Маємо     (cos2x)3/2=(1-sin2x) 3/2.

Перетворивши  ліву частину отриманої рівності і додавши до обох частин число 3,отримаємо

cos3x+3=(1-sin2x) 3/2

Зведемо обидві частини цієї рівності в квадрат

(cos3x+3)2=((1-sin2x) 3/2+3)2

Поклавши в останню рівність х=90о та враховуючи,що cos 90о=0,

sin 90о=1,отримаємо вірну рівність 32=32. Поклавши  до того ж самого рівняння х=180о і враховуючи, що значення cos 180о=-1,а sin 180о=0.виходить

22=42.

Розв’язання. Згідно з формулою корінь квадратний із квадрата не в якій функції рівен не самій функції, а її модулю.

В цьому випадку,звичайно, ніякого софізму не виходить. Так, при х=180о, з урахуванням того, що|cos 180о|=|-1|=1

і sin 180о=0, отримаємо вірну рівність

Приклад 1. Доведемо, що від’ємне число більше додатного.

Візьмемо два додатних числа а і с. Порівняємо два відношення:

а /(-c)    і   (-а )/ c

Вони рівні, так як кожне з них одно - (а / с).  Тоді можна скласти пропорцію:

a /(-c) =(-a) / c

Маємо рівність двох дробів. А якщо у першому дробі чисельник більше за знаменник, то і в другому теж, тому що отримані дроби рівні. У нашому випадку а>-с, отже, повинно бути -а>с, тобто від’ємне число більше додатнього.

Розв’язання. Для додатних чисел використане твердження є правильним, а для від’ємних виконується не для будь-яких відношень. Насправді, з рівності двох дробів а/b=c/d має місце основна властивість пропорції аd=bc, яка даний софізм не доводить.

Приклад 2. В прямокутному трикутнику катет більше гіпотенузи.

Розглянемо довільний прямокутний трикутник АВС і доведемо,що його катет АС більше ніж гіпотенуза ВС.

Для цього запишемо дві очевидні рівності

ВС2–AС2=(ВС+АС)(ВС–АС)

ВС2–AС2= –(ВС+АС)(ВС–АС)

Із якого виходить, що

(ВС+АС)(ВС-АС)= –(ВС+АС)(АС-ВС)

Розділивши останню рівність на –(ВС+АС)(ВС–АС), отримаємо рівність

ВС+Ас/ -(ВС+АС) = АС –Вс/ВС - Ас

В якому в лівій частині дробу чисельник  ВС+АС більше знаменника

–(ВС+АС), також позитивна величина завжди більше ніж негативна. Тому необхідно, щоб і в правій частині виконувалася нерівність АС–ВС>BC–AC,звідки АС+АС>BC+BC, або 2АС>2ВС,або, нарешті.

АС>BC.

Розв’язання. Помилка складається в тому, що порівняння двох дробів необхідно проводити згідно визначенню рівностей дробів, а не порівнювати окремо чисельник та окремо знаменник цих дробів.

Приклад 1. Доведемо, що 4>12

Додаючи до обох частин очевидної нерівності 7> 5 число -8, маємо (7-8)> (5-8), тобто -1> -3 . Помноживши  цю  нерівність  на (-4),  отримуємо

(-1) · (-4)> (-3) · (-4), тобто   4> 12.

Розв’язання. Помилка була допущена при множені нерівності на від’ємне число без зміни знаку нерівності.

Приклад 1. Доведемо, що  64см2=65см2

Візьмемо квадрат зі стороною 8 см и розкладемо його на чотири частини:дві трапеції і два прямокутних трикутника,як показано на малюнку а).

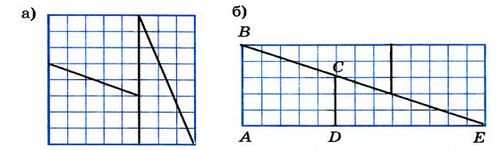
Складуючи ці чотири частини в іншому порядку, а саме так,  як показано на малюнку б), отримаємо прямокутник з основами 13см та висотою 5 см. Площа цього прямокутника дорівнює 5см* 13см=65см2,в той час як площа первісного взятого квадрата (мал. а) дорівнювала 8см*8см=64см2,тоді:

64см2=65см2 

Розв’язання. В софізмі допущена неточність при укладенні частин, складових квадрата. ВЕ тільки здається на око, що вона пряма. Насправді ВЕ являється ламаною, тому що точки В,С і Е не лежать на одній прямій. Щоб переконатися в цьому,достатньо вичислити тангенсі кутів нахилу були б рівні між собою.

Тангенс кута нахилу прямої ВС дорівнює 2/5 =0,4, а прямої 3/8 = 0,375.Ці тангенси не рівні між собою,і тому ВСЕ не пряма,а ламана, тому прямокутник на (мал. б) не рівновеликий квадрату на (мал. а).Легко здогадатися, що між верхніми та нижніми частинами прямокутника (мал. б), віддаленим один від одного прямими ВС та СЕ, мається маленький зазор, площа якого як раз дорівнює 1см2, що и робить площа прямокутника більшою на 1см2 площі квадрата(мал. а). Настільки мала відмінність в тангенсах кутів нахилу прямих ВС і СЕ і пояснює не помітне для ока відхилення один від одного   

Наука про закони і форми мислення називається логікою. Вона допомагає будувати міркування так, щоб дістати істинні результати. Основи формальної логіки заклав  давньогрецький філософ Аристотель. Він показав, що правильні міркування  підпорядковані невеликому числу законів, які не залежать від змісту висловлювань, а тільки від їх форми. Саме тому логіку Аристотеля називають формальною. Одною з задач уроків  математики є розвиток логічного мислення, тобто вміння визначено, послідовно, несуперечливо і доказово міркувати.

Розглянемо  чотири  основні закони  формальної логіки.

Закон тотожності - вимагає,щоб одна і та ж думка,яка наводиться в даному умовиводі, при повторенні мала один і той самий зміст. Багато помилок у міркуваннях пов’язано саме з порушенням цього закону. Вони зумовлені багатозначністю слів, словосполучень і речень природної мови. Наприклад в умовиводі ,,Кожний метал є елементом. Латунь – метал. Отже, латунь є елементом” неправильний висновок, обумовлений недотриманням закону   тотожності:  в двох значеннях використано ім’я ,,метал”. У першому реченні – в    значенні хімічного елемента, в другому йдеться про сплав металів – речовину, яка має фізичні властивості металу: ковкість, металевий блиск, електропровідність.

Закон суперечності  полягає в тому, що не можуть бути одночасно істинним два протилежні висловлення про один і той самий об’єкт, взятий в один і той самий час і в одному й тому самому розумінні. Отже, не можна одночасно стверджувати й заперечувати щось про один і той самий об’єкт, бо такі висловлення не можуть одночасно бути істинними.

Закон суперечності пов’язаний з так званим контрарними протилежностями. Це вид протилежностей. коли зіставляється загальностверджувальне і загальнозаперечувальне висловлювання. Наприклад «Всі ромби – опуклі чотирикутники» і «Жоден ромб не є опуклим чотирикутником».

Закон виключеного третього стверджує,що з двох суперечливих висловлень, де розглядається один і той самий об’єкт в один і той самий час, одне обов’язково істинне. Наприклад, загальностверджувальне  і загальнозаперечувальне висловлювання («Всі парні числа складені», «Деякі парні числа не є складеними»).

Закон достатньої підстави вимагає, щоб кожна істинна думка була обґрунтована іншими думками, істинність яких доведено. Цей закон відображає одну з фундаментальних властивостей світу: в природі,частиною якої є людина, нема безпричинних явищ, кожне явище виникає із якихось інших фактів та явищ.

У казці Л. Керрола можна знайти чудові приклади «доведень», у процесі якіх герої порушують закон достатньої підстави. Наприклад:

1. Зніми свого капелюха, – сказав Король Капелюшнику.
2. Він не мій, – відповів Капелюшник
3. Вкрадений! – закричав Король з торжеством і повернувся до присяжних,    які тут взялися за грифелі.
4. Я їх тримаю для продажу, – пояснив Капелюшник. – У мене своїх нема, адже я Капелюхових справ Майстер.

Справжній урок математики одночас є уроком розвитку грамотного мовлення. Тому на доцільне використовувати приклади  мовних софізмів, пов’язаних  з порушенням законів логіки ( в основному, закону тотожності).

Двозначність слова. Як правило кожне поняття в математиці позначається своїм особливим терміном. У виняткових випадках,тобто коли один и той самий термін використовується в різних значеннях,необхідні спеціальні вказівки,в якому самому сенсі тут використовується даний термін,якщо не зрозуміло із самого контексту.

До числа неоднозначних математичних термінів відноситься, наприклад, наступне: квадрат(показник степеня і геометрична фігура,корінь(в сенсі рішення рівняння и як синонім до слова радикал), число (кількісне та порядкове,абстрактне та  іменоване, точне і приблизне).

Приклад. Батько та син прибули до міста на постійне місце проживання. Хлопчик із розказу батьків знав,що в місті живе 25 тис. жителів, поспішивши на вокзалі заявити,що зараз у місті жителів 25002.Батько засміявся та щось пояснив сину. Що сказав він хлопчику?

Двозначність вимови, тобто спотворення первинного сенсу фрази через  зміну постановки наголосу в будь-якому слові.

Приклад. Сто сорок да сто сорок буде двісті сорок.

Двозначність конструкції, тобто використання  такої  конструкції  речення, яка допускає різне сприйняття його змісту.

Приклад. Скільки буде тричі три та сім?

Зі змістом цієї фрази узгоджуються два різних, один одного виключаючих, порядку дій, а саме 3 * 3 +7 і 3 * (3 +7)

Помилка розподілу. Ця помилка має місце, коли терміну,  вжитому в збірному сенсі, надається значення розділового.

Приклад. Всі кути трикутника дорівнюють двом прямим кутам.

Тут слово «всі» вжито в значенні  «сума».  Однак вибір терміна невдалий, оскільки можна його розуміти і в сенсі   «кожен». Думка стає абсурдною: «Кожен кут трикутника дорівнює сумі двох прямих кутів».

Помилка складання. Помилка, протилежна попередній. Вона виникає тоді, коли терміни, вжиті в розділовому сенсі, надається значення збірного.

Приклад. Всі кути трикутника менше двох прямих кутів.

Тут слово  «всі» вжито в значенні «кожен». Однак вибір терміна не можна визнати вдалим, так як його можна розуміти і в сенсі «сума».  Думка для системи евклідової геометрії стає абсурдною: «Сума кутів трикутника менше двох прямих кутів».

Дуже багато  мовних софізмів виглядають як позбавлена ​​сенсу і мети гра з мовою; гра, яка спирається на багатозначність мовних виразів, їх неповноту, недомовленість, залежність їх значень від контексту і т.д. Ці софізми здаються особливо наївними і несерйозними, але від цього не менш цікавішими для учнів. Наведемо декілька прикладів таких відомих мовних софізмів.

Софізм «Не знаєш те, що знаєш»:
-Чи знаєш ти, про що я хочу тебе запитати?
- Ні.
- Чи знаєш ти, що доброчесність є добро?
- Знаю.
- Про це я і хотів тебе запитати. А ти, виходить, не знаєш те, що знаєш

Софізм «Ліки». Ліки, прийняті хворим, є добро. Чим більше робити добра, тим краще. Значить, ліків потрібно приймати якомога більше.

Софізм «Чим більше», який став пісенькою англійських студентів:

Софізм «Напівпорожнє і напівповне».  Напівпорожнє  є те ж, що інапівповне. Якщо дорівнюють половини, значить, рівні та цілі. Отже, порожнє є те ж, що і повне.

Розбір помилок мови в школі вважаю дуже корисним для виховання в учнів поваги до кожного слова, математичного твердження та формулювань теорем.

Таким чином я розглянув найбільш цікаві математичні софізми та парадокси, які можна використовувати на уроках математики. Розбір помилок, припущених у софізмах, є потужним інструментом для розвитку критичного та логічного мислення учнів, «профілактики» припущення таких помилок у подальшому.

Крім того, такі завдання  можуть бути використані при вивченні історичного аспекту теми, створення проблемної ситуації, для повторення вивченого матеріалу. Але треба зазначити, що для сприйняття математичних софізмів учні повинні мати добру математичну підготовку. Педагоги-фахівці не радять вказувати на можливі помилки на початку вивчення теми. Розглядати такі завдання з «прихованою» помилкою бажано на підсумкових уроках.

Для розв’язання математичних софізмів можна використати наступні  рекомендації:

Уважно прочитайте  умову запропонованої задачи.  Розпочати пошук помилки краще з умови, бо в деяких софізмах абсурдний результат отримується завдяки наявних протиріч в умові, неповних даних, неправильного малюнка.  А всі наведені далі міркування є вірними.

Встановити область знань ( теми), які відображені у софізмі, запропоновані перетворення. Софізм може мати декілька розділів, кожен з яких потребує детального аналізу.

З’ясуйте, чи виконані  всі умови застосування теорем, правил, формул, дотримуються закони логіки.  Деякі софізми побудовані на невірному використанні означень, законів, на «забуванні» умов  застосування. Дуже часто при вивченні властивостей математичних об’єктов запам’ятовуються лише основні фрази, а все інше  - забувається (наприклад,  саме таким чином друга ознака рівності трикутників  перетворюється на ознаку «по стороні та двом кутам»)

Перевірте  правильність перетворень оберненими діями.

Часто  необхідно поділити приклад на невеликі блоки та проконтролювати правильність кожного такого блоку.

Під час написання даної роботи я знайомив учнів мого класу з деякими софізмами, в яких була «прихована» помилка ділення на нуль (під час повторення теми «Тотожні перетворення алгебраїчних виразів»), неправильне здобування квадратного кореня з квадрату (під час вивчення теми «Степенева функція»), ділення нерівності на від’ємне число без зміни знаку нерівності ( під час вивчення теми «Розв’язання нерівностей») тощо.

Результати вихідного діагностування показали, що більшості учнів стало свідомо зрозуміло до яких «катастрофічних» висновків можуть призводити такі помилки. Крім того, учні відмітили, що розв’язування  софізмів їм дуже сподобалося та зацікавило.

В рамках мети дослідження мною був вивчений історичний аспект виникнення софізмів та з’ясовано, що софізми, як математичні об’єкти виникли у Давній Греції і вже багато років «бентежать» найвитонченіші уми математиків. Софізми є сумішшю математики та філософії, їх вивчення та дослідження було дуже цікавою вправою. Деякі  софізми дійшли до нас з часів Давньої Греції, деякі виникли не так давно. Мною були розглянуті приклади деяких історичних софізмів, які носять ім’я філософів Давньої Греції.  Софізми, або «нездоланні» помилки давали поштовх для розвитку цілих розділів математичної науки.

Мене дуже зацікавила дана тема, а її актуальність була підтверджена дослідженням, яке я провів серед учнів мого класу.

Мною був здійснений аналіз літератури з даного питання, який  показав, що математики використовували різні характеристики для класифікації софізмів: від чисто зовнішніх ознак до характеру припущених помилок. Мною при розгляданні прикладів математичних софізмів була використана класифікація за характером припущених помилок, найбільш розповсюджених серед учнів при вивченні математики.

Аналіз софізмів  показав, що найбільш розповсюдженими помилками, «замаскованими» в математичних софізмах є ділення на нуль; знаходження квадратного кореня з повного квадрату; неправильні  висновки з рівності дробів. В своїй роботі я розглянув найбільш цікаві математичні та логічні софізми та навів їх пояснення.

Реалізуючи поставлену мету моєї дослідницької роботи з математики "Математичні софізми" 10 клас, я дійшов до висновків, що застосування софізмів на уроках математики значно підвищує їх ефективність, тому що розвиває навички логічного мислення;  допомагає свідомому засвоєнню математики, розвиває спостережливість, критичне відношення до того, що вивчається.  Крім того,  розуміння  помилок в софізмі веде до  свідомого розуміння математики в цілому, допомагає запобігти припущенню відповідних  помилок у подальшому. Це підтвердили також результати вихідного діагностування учнів мого класу.

Новизна мого дослідження полягає в тому, що мною була зроблена класифікація софізмів за характером припущених помилок та відповідно до шкільного курсу математики. Розглянуті  у роботі приклади будуть цікаві, в першу чергу, учням середньої школи, бо «приховані» в них помилки ідуть всупереч з добре відомими усім  фактами. Окрім того, мною були надані деякі рекомендації щодо розв’язування задач, пов’язаних з софізмами.

Таким  чином мета мого дослідження в рамках дослідницького проєкту з математики на тему "Математичні софізми" досягнута. Проте, багато цікавих софізмів не було ще розглянуто. І зараз народжуються безліч парадоксів та софізмів, які чекають свого розв’язання. Тому обрана мною тема є невичерпним джерелом для отримання інтелектуального задоволення  та гімнастики розуму.

Адресую свою дослідницьку роботу з математики "Математичні софізми" учням середньої школи та вчителям математики.

1. А. Г. Мадера «Математические софизмы».
2. Литцман В., Трир Ф. «Где ошибка?» - СПб., 1919.
3. Математические софизмы и парадоксы А. Г. Конфорович.
4. Брадис В.М., Минковский В.Л., Харчева А.К. Ошибки в математических рассуждениях.